백준 1915 가장 큰 정사각형 with Python

문제 링크

알고리즘

• 다이나믹 프로그래밍

풀이

큰 정사각형을 작은 정사각형 3개로 나눌 수 있다는 아이디어로 해결할 수 있다.

[문제] 아래와 같은 문제가 주어졌을 때, 빨간색 1을 포함한 정사각형의 크기를 생각해보자. (3x3이 나올 것이다)

빨간색 1의 왼쪽, 왼쪽 위 대각선, 위의 숫자들 각각이 포함된 정사각형의 크기를 구하고, 이를 이용해서 위의 문제를 해결할 수 있다. (오른쪽과 아래는 무시한다)
표현하면 다음과 같다. 왼쪽, 왼쪽 위 대각선, 위 각각 3x3, 2x2, 3x3의 크기를 가지고 있다.

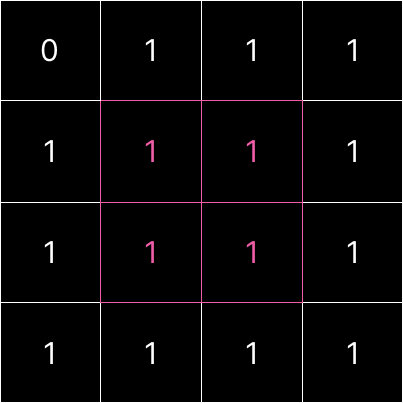
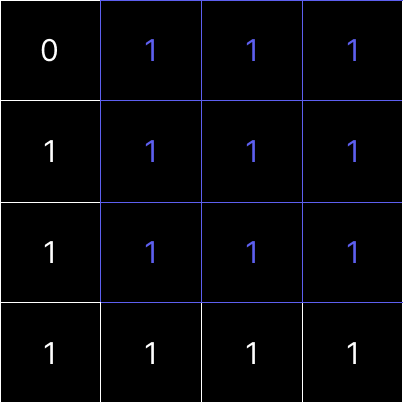
이렇게 나온 3,2,3 중 최솟값(2)을 뽑고 1을 더하면 원래 구하려던 빨간색 1이 포함된 정사각형의 크기(3)를 구할 수 있다.

위에서 했던 것을 모든 원소에 적용하면 다음과 같다. 각 숫자는 왼쪽, 왼쪽 위 대각선, 위만을 고려하고 각 원소가 포함된 정사각형의 크기를 구한 값이다. (오른쪽과 아래는 무시한다)

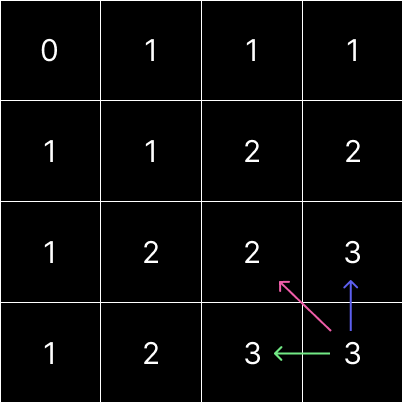
위를 구하고 전체 리스트의 최댓값을 구하면 문제의 답이 나온다.

전체 코드

import sys

input = sys.stdin.readline

n, m = map(int, input().split())

arr = [list(map(int, list(input().strip()))) for _ in range(n)]

dp = [[0] * m for _ in range(n)]

res = 0


for i in range(n):
    for j in range(m):
        if arr[i][j] == 0:  # 주어진 배열의 값이 0이면 크기도 0
            dp[i][j] = 0
        else:
            prev_col = 0 if j == 0 else dp[i][j - 1]  # 왼쪽
            prev_row = 0 if i == 0 else dp[i - 1][j]  # 위
            prev_diag = 0 if i == 0 or j == 0 else dp[i - 1][j - 1]  # 왼쪽 위 대각선
            dp[i][j] = min(prev_row, prev_col, prev_diag) + 1  # 최솟값을 뽑고 1을 더한다.
            res = max(res, dp[i][j]) # 최댓값 갱신

print(res**2)

후기

이분 탐색을 포함해서 총 5가지의 방법을 시도해보고 겨우 정답을 찾았다. 다이나믹 프로그래밍은 풀고 풀어도 정말 어려운 것 같다. (이 문제를 이분 탐색으로 풀면 O(N^4) * O(logN)의 시간 복잡도가 나온다. N이 1000으로 작긴 해도 시간 초과가 난다.)